Les étoiles : Mesure de température

Afin de mettre en œuvre une détermination expérimentale de la température des étoiles, via leur couleur, donc via une mesure spectroscopique, nous avons mené quelques expériences d'optique géométrique, puis ondulatoire.

TP1 - 0ptique géométrique

Nous avons réalisé un TP d'introduction à l'optique géométrique. Avec une lumière rouge monochromatique (faisceau laser). Une source de lumière monochromatique est caractérisée par une seule fréquence, donc une seule longueur d’onde dans le vide : nous étudions donc d'abord la déviation des rayons due au changement d'indice du milieu (air/plexiglas), sans effet de dispersion (déviation de la lumière selon sa longueur d'onde).

Nous avions utilisé un demi cercle de plexiglas gradué. La loi de Snell-Descartes a pu être vérifiée expérimentalement. En effet le rayon lumineux du laser arrivant sur un dioptre a alors été réfracté sur le plan d'incidence selon les lois suivantes :

• Le rayon réfracté se situe dans le plan d'incidence (défini par le rayon incident et la normale au dioptre au mouvement d'incidence), rayon incident et rayon réfracté étant de part et d'autre de la normale ;
• Les angles d'incidence et de réfraction (i₁) et (i₂), mesurés par rapport à la normale sont tels que :

                                                           n1.sin(i₁)= n2.sin(i₂)

Ceci nous a permis de mesurer l'indice n du plexiglas en réalisant une campagne de mesures.



Séance du 6 Mai: Nous avons mesuré l'indice de réfraction grâce à la loi de Snell-Descartes : 
   n1.sin(i₁)= n2.sin(i₂)

Traitement statistique :
valeur moyenne : <n2>= 1.43
écart-type : σ (n2)= 0.12
On donne donc le résultat avec son incertitude : 
n2= <n2> + Δn2 
avec  Δn2 = k x σ(n2) /sqrt(N) et N=8 le nombre de mesures réalisées
Pour N=8, le facteur d'élargissement de Student pour un intervalle de confiance à 95% vaut k(0.95)= 2.03 d'après la table de Student.
Δn2 =2.03 x 0.12/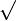8= 0.09
Donc n2= 1.43 ± 0.09

Nous cherchons à savoir si nous avons effectué une bonne mesure. L'incertitude relative de notre mesure est
Δn2/n2 =0.09/1.43= 0.06, soit 6% d'erreur.


Utilisation de lentilles minces et de fentes afin de réaliser une image nette sur un écran :

Pour obtenir une image nette sur un écran, il faut conjuguer l'objet (fente éclairée par une lampe) et l'écran grâce à une lentille convergente, qui collecte la lumière incidente et la focalise sur l'écran de façon stigmatique (i.e. pour un point objet, la lentille produit un unique point image).



TP2 - Optique ondulatoire :

Diffraction d'un faisceau laser par un réseau :

On peut aussi diffracter de la lumière blanche à travers un réseau : pour cela, on focalise grâce à une lentille convergente l'image d'une fente sur un écran, en faisant passer le faisceau lumineux à travers un réseau contenant 1000 traits par millimètre. On observe alors une décomposition de la lumière visible. Dans ce cas, on obtient un spectre continu : le spectre de la lumière blanche contient donc toutes les longueurs d'onde du visible. La tâche centrale contient les mêmes longueurs d'onde que les zones diffractées étalées de part et d'autre.

Si au contraire on utilise une source spectrale (ici, lampe à mercure Hg), la lumière produite correspond uniquement aux longueurs d'onde que la vapeur de mercure de l'ampoule peut produire (par désexcitation des atomes ayant absorbé de l'énergie). On observe donc des raies bleues et vertes, mais pas de rouge par exemple. Cela signifie que chaque type de source (par exemple, une étoile) est caractérisée par son spectre d'émission lumineuse, qui dépend des gaz qu'elle contient.

Enfin, voici le résultat de la diffraction d'une lampe à sodium (Na) par le même réseau : on n'observe que des raies jaunes. On en déduit que la vapeur de sodium présente un spectre principalement centré sur le jaune (longueur d'onde entre 560 et 600 nm) :

Soirée d'observation à l'Observatoire de Paris

Le 11 mars 2014, nous sommes allés à l'Observatoire de paris, où nous avons été accueillis par Pacôme Delva, enseignant-chercheur en astronomie. Nous avons tout d'abord visité le bâtiment historique de l'Observatoire (construit sous le règne de Louis XIV), puis nous avons réalisé des observations de la Lune, de Jupiter et de plusieurs étoiles avec un télescope (composé de miroirs), puis avec la lunette astronomique Arago (composée de lentilles) située dans la grande coupole de l'Observatoire, sur les toits de Paris !

Voici quelques photos prises lors de cette sortie :

 Cette photo représente l'observatoire de Paris selon une gravure d'époque :



Sur cette photo on peut observer l'avenue de l'observatoire où le méridien de Paris traverse l’Observatoire en son centre :

                                      

Nous avons pu observer la Lune grâce à un télescope.Nous pouvons observer des cratères de différentes tailles mais aussi le terminateur qui est la séparation de la zone éclairée et la zone d'ombre de la lune.

Ces photos représentent une lunette astronomique. Située dans la coupole.
Cette lunette est posée sur une charpente métallique fixée sur la paroi de la tour,
Cet instrument de 38cm de diamètre et de 9m de focale a été mis en service en 1854.
Lors de cette nuit à l'observatoire, nous, visiteurs chanceux avons pu observer Jupiter et ses satellites.

TP3- Étude des spectres d'étoiles mesurés à l'Observatoire de Paris

Aïe ! Malheureusement le réseau que nous avons voulu utiliser avec notre télescope était trop dispersif, et les raies de diffraction par le réseau n'étaient pas visibles quand nous avons branché notre appareil photo sur l'objectif accolé au réseau. Donc la mesure n'est finalement pas été possible, mais ce n'est que partie remise !

Pour se donner une idée, la figure ci-dessous montre que les étoiles que nous connaissons ont des couleurs variées, et n'ont donc pas du tout la même température de surface !