La Lune : Mesure de la profondeur des cratères

Nous nous sommes intéressés au cratère présent sur la Lune, et nous nous sommes posés la question suivante:

Comment peut-on mesurer la profondeur d'un cratère lunaire ?

Pour répondre à cette question nous avons schématisé notre problème avec un dessin:

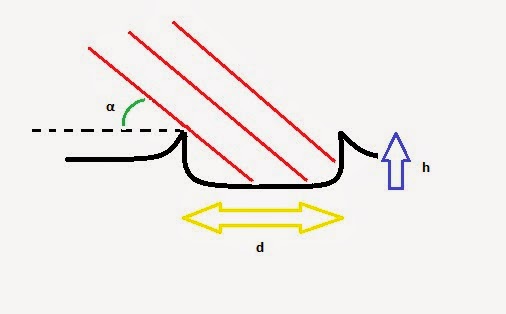Schéma représentant le moyen de calculer la profondeur h d'un cratère.

Sur ce schéma, "d" représente l'ombre crée par le rebord du cratère (le lecteur attentif aura remarqué qu'il y a donc une petite erreur sur le schéma !), "h" est la profondeur du cratère, et α représente l'angle formé par les rayons du soleil (ici représentés par des traits rouges) et l'horizontale.

En appliquant une simple formule de trigonométrie, on obtient la formule suivante :
 tan(α) = h / d

En prenant une photo de bonne résolution d'un cratère lunaire, on peut donc mesurer la taille de l'ombre en connaissant la résolution de notre appareil. Cependant nous ne pouvons mesurer α avec une simple photo d'un cratère. Il faut donc trouver un moyen de mesurer cet angle.

Pour ce faire, nous devons sélectionner un cratère proche du terminateur. Le terminateur est le côté "sombre" de la Lune. Voici un dessin schématisant la situation afin de mieux comprendre l'utilité d'une photo avec notre cratère et le terminateur:

Schéma représentant la méthode de mesure de α

Sur ce schéma, R représente le rayon de la Lune (environ 1737.4 km), Rt la distance entre le terminateur et notre cratère, celui-ci étant le point rouge sur notre schéma.
Grâce à ce schéma, on obtient la formule suivante: sin (α) = Rt / R
Ainsi on obtient: α = arcsin (Rt / R)

Une fois α mesuré, nous pouvons revenir sur notre calcul de la profondeur h du cratère :

h = d . tan (α)

Ainsi avec une photo de la Lune sur laquelle nous pouvons voir à la fois notre cratère et le terminateur, nous avons la possibilité de déterminer la profondeur h du cratère choisi.

Comment exploiter une photo?

Nous avons, lors d'une sortie scolaire à l'Observatoire de Paris, pris des clichés de la Lune grâce à une lunette astronomique.
 

Nous savons que la Lune à un diamètre de 1737 km. Nous avons donc essayer de trouver à combien de pixel cela correspondait sur la photo, ainsi que la valeur en mètre dans la vrai vie d'un pixel de cette photo.

On a appliqué la formule suivante: 

Sqrt(L^2+H^2)=Le nombre de pixels de la photo

On a obtenue les résultats suivant:

- Ahmed: 721 m

- Kenza: 717 m

- Jessica: 725 m

-Asif et Leavens: 726 m

La moyenne de nos résultat est 722.3 m. Nous avons donc 1 pixel correspondant à 722.3 m sur notre photo.

Exploitation du cliché:

Nous savons donc que dans notre photo, 1 pixel vaut 722.3 m. Nous avons aussi trouvé les formules suivante:

α = arcsin (Rt / R)
h = d . tan (α)

Nous avons effectuer les calculs sur 4 cratères différents:

cratère 1: Rt (en m)= 471491.5 ; d (en m)= 30729.6 ; on obtient donc h= 4209 m
Ce cratère à une profondeur de 4209 mètres.

cratère 2: Rt (en m)= 281326.3 ; d (en m)= 28206.7 ; on obtient donc h= 2291 m
Ce cratère à une profondeur de 2291 mètres.

cratère 3: Rt (en m)= 432853 ; d (en m)= 30380 ; on obtient donc h= 3815 m
Ce cratère à une profondeur de 3815 mètres.

cratère 4: Rt (en m)= 437714 ; d (en m)= 15168 ; on obtient donc h= 1926 m
Ce cratère à une profondeur de 1926 mètres.

Nos 4 cratères, pris au hasard sur la surface lunaire, ont une profondeur comprise entre 1.9 et 4.2 km. En comparaison, le Mont Blanc fait 4810 m d'altitude, donc certains cratère lunaire pourraient sans doute contenir le Mont Blanc !